Universal Properties in the Energy Spectrum of Semiconductor Quantum Dots

Abstract

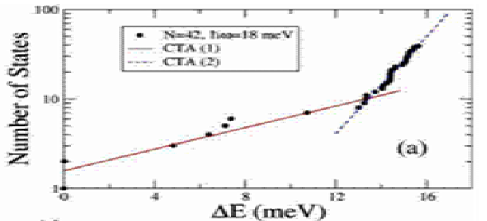
In a two-dimensional parabolic quantum dot charged with N electrons, Thomas-Fermi theory states that the ground-state energy satisfies the following non-trivial relation: E_gs/(ℏω) ≈ N^3/2f_gsN^1/4β, where the coupling constant, β , is the ratio between Coulomb and oscillator (ℏω) characteristic energies, and f_gs is a universal function. We perform extensive Configuration Interaction calculations in order to verify that the exact energies of relatively large quantum dots approximately satisfy the above relation. In addition, we show that the number of energy levels for intraband and interband (excitonic and biexcitonic) excitations of the dot follows a simple exponential dependence on the excitation energy, whose exponent, 1/ϴ , satisfies also an approximate scaling relation a lá Thomas-Fermi, ϴ/ℏω ≈ N^-ϒg(N^1/4β). We provide an analytic expression for f_gs , based on two-point Padé approximants, and two-parameter fits for the g functions. The structure of the numerical library Libqdot, as well as the role of each Fortran 90 module is explained.