Abstract
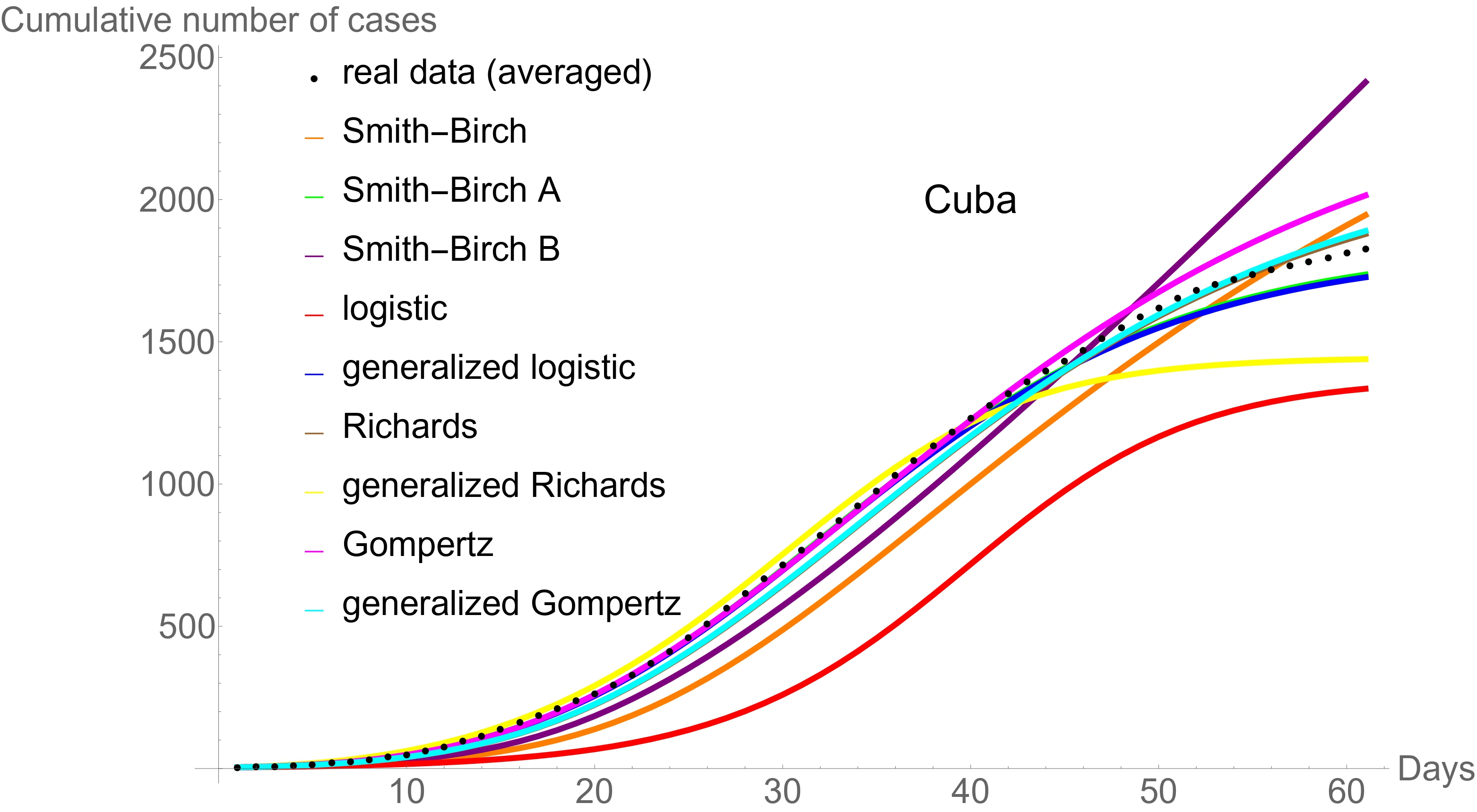
S-shaped or sigmoid curves can be defined as the solutions of autonomous first-order differential equations that satisfy four conditions. Without solving the equations, we demonstrate that the solutions of the logistic family and the Smith-Birch model satisfy these conditions. We introduce two generalizations of the Smith-Birch, whose solutions are identified as S-shaped for some range of variation of the parameters. The new models introduced here predict the spread of the disease better than traditional logistic family models for time series of the cumulative number of cases for the first 61 days of the COVID-19 pandemic in some countries.
References
[1] V. Vieira, Comput. Ecol. Soft. 10, 162 (2020).
[2] F. H. Eeckman and W. J. Freeman, Brain Res. 557, 13 (1991).
[3] K. Sandberg, B. M. Bibby, B. Timmermans, A. Cleeremans, and M. Overgaard, Conscious. Cogn. 20, 1659 (2011).
[4] D. R. F. Paul E. Smaldino, Lucy M. Aplin, Sci. Rep. 8, 14015 (2018).
[5] J. M. J. Murre, Psychon. Bull. Rev. 21, 344 (2014).
[6] C. L. T. D. Tab Rasmussen, J. Hum. Evol. 23, 159 (1992).
[7] H. Qiu, K. Durand, H. Rabinovitch-Chable, M. Rigaud, V. Gazaille, P. Clavère, and F. G. Sturtz, Biotechniques 42, 355 (2007).
[8] S. Pixton and R. Howe, J. Stored. Prod. Res. 19, 1 (1983).
[9] A. G. A. Anna M. Michałowska-Kaczmarczyk and Tadeusz Michałowski, J. Anal. Sci., Methods and Instrumentation 4, 27 (2014).
[10] C. Y. Hsieh, S. L. Fang, Y. F. Wu, Y. C. Chu, and B. J. Kuo, Hortic. 7, 537 (2021).
[11] S. H. Austin, T. R. Robinson, W. D. Robinson, and R. E. Ricklefs, Methods Ecol. Evol. 2, 43 (2011).
[12] M. Michalczu, K. Damaziak, and A. Goryl, Ann. Anim. Sci. 16, 65 (2016).
[13] L. Cao, P.-J. Shi, L. Li, and G. Chen, Symmetry 11, 204 (2019).
[14] T. Onoda, R. Yamamoto, K. Sawamura, Y. Inoue, A. Matsui, T. Miyake, and N. Hirai, J. Equine Sci. 22, 37 (2011).
[15] Y. Zhang, A. Biswas, and V. I. Adamchuk, Geoderma 289, 1 (2017).
[16] K. Hufkens, R. Ceulemans, and P. Scheunders, Ecol. Inform. 3, 97 (2008).
[17] B. G. Akre and D. M. Johnson, J. Anim. Ecol. 48, 703 (1979).
[18] J. I. Lehr Brisbin and M. C. Newman, Water Air Soil Poll 57-58, 691 (1991).
[19] L. A. Kuznar and W. G. Frederick, Ecol. Econ. 46, 296 (2003).
[20] I. McGowan, The Statistician 35, 73 (1985).
[21] K. Kobayashi, W. A. Borders, S. Kanai, K. Hayakawa, H. Ohno, and S. Fukami, Appl. Phys. Lett. 119, 132406 (2021).
[22] D. S. Paolino and M. P. Cavatorta, Fatigue Fract. Eng. Mater. Struct. 36, 316 (2012).
[23] M. El-Khawaga, S. El-Badawy, and A. Gabr, Arabian J. Sci. Eng. 45, 3973 (2020).
[24] S. Mastilovíc, Theor. Appl. Mech. 45, 95 (2018).
[25] D. Jang, G. Chae, and S. Shin, Sens. 15, 25385 (2015).
[26] B. Lu, H. He, H. Yu, H.Wang, G. Li, M. Shi, and Dongpu, Sens. 20, 7197 (2020).
[27] D. Kucharavy and R. D. Guio, Procedia Eng. 9, 559 (2011).
[28] R. Bürger, G. Chowell, and L. Y. Lara-D´ıaz, Math. Biosci. 334 (2021), ISSN 18793134.
[29] F. Brauer, C. Castillo-Chavez, and Z. Feng, Mathematical Models in Epidemiology, Texts in Applied Mathematics (Springer, New York, NY, 2019).
[30] G. Zhou and G. Yan, Emerg. Infect. Dis. 9 (2003), ISSN 10806040.
[31] B. Pell, Y. Kuang, C. Viboud, and G. Chowell, Epidemics 22 (2018), ISSN 18780067.
[32] D. W. Shanafelt, G. Jones, M. Lima, C. Perrings, and G. Chowell, EcoHealth 15 (2018), ISSN 16129210.
[33] L. Dinh, G. Chowell, K. Mizumoto, and H. Nishiura, Theor. Biology Med. Model. 13 (2016), ISSN 17424682.
[34] S. Zhao, S. S. Musa, H. Fu, D. He, and J. Qin, Parasit. Vectors. 12 (2019), ISSN 17563305.
[35] B. Malavika, S. Marimuthu, M. Joy, A. Nadaraj, E. S. Asirvatham, and L. Jeyaseelan, Clin. Epidemiol. Glob. Health. 9 (2021), ISSN 22133984.
[36] C. Y. Shen, IJID 96 (2020), ISSN 18783511.
[37] K. Wu, D. Darcet, Q. Wang, and D. Sornette, medRxiv (2020).
[38] G. L. Vasconcelos, A. M. Macdo, R. Ospina, F. A. Almeida, G. C. Duarte-Filho, A. A. Brum, and I. C. Souza, Peer J 2020 (2020), ISSN 21678359.
[39] K. Roosa, Y. Lee, R. Luo, A. Kirpich, R. Rothenberg, J. M. Hyman, P. Yan, and G. Chowell, J. Clin. Med. 9 (2020), ISSN 20770383.
[40] K. Roosa, Y. Lee, R. Luo, A. Kirpich, R. Rothenberg, J. M. Hyman, P. Yan, and G. Chowell, Infect. Dis. Model. 5 (2020), ISSN 24680427.
[41] Y. Wu, L. Zhang, W. Cao, X. Liu, and X. Feng, Front. Phys. 8, 566 (2021), ISSN 2296-424X.
[42] M. López, A. Peinado, and A. Ortiz, PLoS ONE 16
(2021), ISSN 19326203.
[43] P. Pincheira-Brown and A. Bentancor, Epidemics 37 (2021), ISSN 18780067.
[44] M. T. Pérez-Maldonado, J. Bravo-Castillero, R. Mansilla, and R. O. Caballero-P´erez, Nova scientia 14, 18 (2022).
[45] G. Jarne, J. Sanchez-Choliz, and F. Fatas-Villafranca, Evol. Inst. Econ. Rev. 3, 239 (2007).
[46] L. S. Pontriaguin, Ecuaciones Diferenciales Ordinarias (Editorial Pueblo y Educación, La Habana, 1981).
[47] M. Carrillo and J. M. González, Technol. Forecasting Social Change 69, 233 (2002).
[48] W. G. Bardsley and R. E. Childs, Biochem. J. 149, 313 (1975).
[49] Z. Li, B. S. Yang Zhang, Z. Xing, and Q. Wang, Electronics 11, 1365 (2022).
[50] R. Gomeni and C. Gomeni, Comput. Biomed. Res. 13, 489 (1980).
[51] H. Li, X. Jiang, G. Huo, C. Su, B. Wang, Y. Hu, and Z. Zheng, nt. J. Adv. Manuf. Technol. 119, 1531 (2022).
[52] P. Verhulst, Corr. Math. Physics 10, 113 (1838).
[53] A. Tsoularis and J. Wallace, Math. Biosci. 179 (2002), ISSN 00255564.
[54] M. H. Zwietering, I. Jongenburger, F. M. Rombouts, and K. van’t Riet, Appl. Environ. Microbiol. 56, 1875 (1990).
[55] J. Schnute, Can. J. Fish. Aquat. Sci. 38, 1128 (1981).
[56] K. M. C. T. Erve and E. T. Erve, Ecol. Modell. 359, 117 (2017).
[57] F. E. Smith, Ecol. 44, 651 (1963).
[58] C. P. D. Birch, Ann. Bot. 83, 713 (1999).
[59] M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (Dover, New York, 1964), ninth dover printing, tenth gpo printing edition.
[60] R. M. May, Nature 261, 459 (1976), ISSN 20522541.
[61] W. E. Boyce and R. C. DiPrima, Elementary Differential Equations (John Wiley & Sons, Inc., Hoboken, NJ, 2012).
[62] A. L.-M. J. A. Mesejo-Chiong, Ciencias Matemáticas 34, 19 (2020).

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Copyright (c) 2025 Cuban Physical Society & Faculty of Physics of the University of Havana