Eight-Centered Oval Quasi-Equivalent to Kepler’s Ellipse of Planets’ Prajectory

Abstract

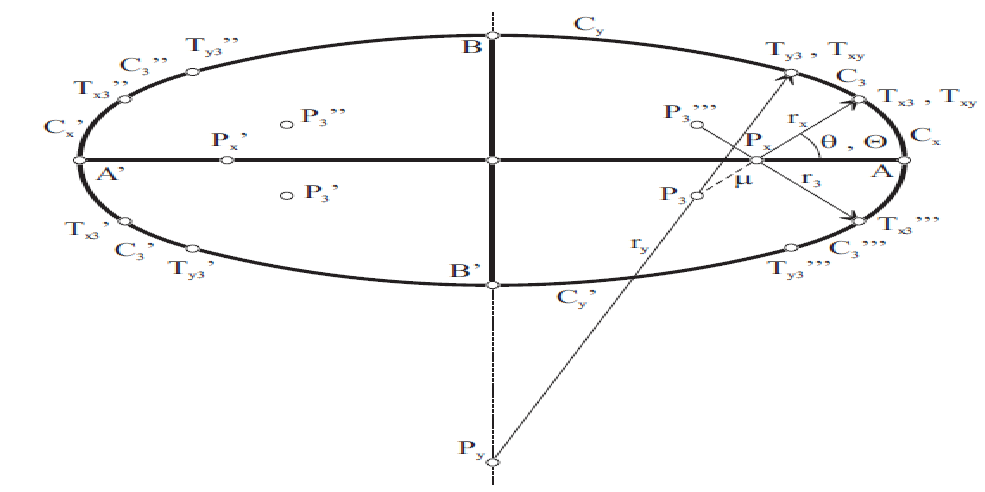
This paper has academic nature, nevertheless it is an application from [9] that we think can be interesting  to students and instructors of undergraduate level of physics. With low level of geometric and computational techniques the readers can reproduce the results of the present paper. The most important thing is that these results clearly show that it is not enough take numerical measures of the orbits of the bodies to decide which are the real equations and laws that govern them. We present an approximation of the Kepler’s ellipse of the planets’ trajectory by circular arcs, which is quasi-equivalent; that is: we present the approximation of the Kepler’s ellipse ε_b by the eight-centered oval O_εb having the same center, axes, vertices, perimeter length and curvature at the vertices as ε_b, and also having practically negligible difference with respect to the surface area of ε_b, and also having barely distinguishable deformation error in relation to ε_b.